Определение двойного интеграла. Двойной интеграл

Свойства двойных интегралов.

Часть свойств двойных интегралов непосредственно вытекает из определения этого понятия и свойств интегральных сумм, а именно:

1. Если функция f(x, y) интегрируема в D , то kf(x, y) тоже интегрируема в этой области, причем (24.4)

2. Если в области D интегрируемы функции f(x, y) и g(x, y) , то в этой области интегрируемы и функции f(x, y) ± g(x, y) , и при этом

3. Если для интегрируемых в области D функций f(x, y) и g(x, y) выполняется неравенство f(x, y) ≤ g(x, y) , то

(24.6)

Докажем еще несколько свойств двойного интеграла :

4. Если область D разбита на две области D 1 и D 2 без общих внутренних точек и функция f(x, y) непрерывна в области D , то

(24.7) Доказательство . Интегральную сумму по области D можно представить в виде:

где разбиение области D проведено так, что граница между D 1 и D 2 состоит из границ частей разбиения. Переходя затем к пределу при , получим равенство (24.7).

5. В случае интегрируемости на D функции f(x, y) в этой области интегрируема и функция | f(x, y) | , и имеет место неравенство

(24.8)

Доказательство.

откуда с помощью предельного перехода при получаем неравенство (24.8)

6. где S D – площадь области D. Доказательство этого утверждения получим, подставляя в интегральную сумму f(x, y) ≡ 0.

7. Если интегрируемая в области D функция f(x, y) удовлетворяет неравенству

m ≤ f(x, y) ≤ M ,

то (24.9)

Доказательство.

Доказательство проводится предельным переходом из очевидного неравенства

Следствие.

Если разделить все части неравенства (24.9) на D , можно получить так называемую теорему о среднем:

В частности, при условии непрерывности функции f в D найдется такая точка этой области (х 0 , у 0 ), в которой f (х 0 , у 0 ) = μ , то есть

Еще одна формулировка теоремы о среднем.

Геометрический смысл двойного интеграла.

Рассмотрим тело V , ограниченное частью поверхности, задаваемой уравнением z = f(x, y), проекцией D этой поверхности на плоскость Оху и боковой цилиндрической поверхностью, полученной из вертикальных образующих, соединяющих точки границы поверхности с их проекциями.

z=f(x,y)

y P i D Рис.2.

Будем искать объем этого тела как предел суммы объемов цилиндров, основаниями которых являются части ΔS i области D , а высотами – отрезки длиной f (P i ), где точки P i принадлежат ΔS i . Переходя к пределу при , получим, что

(24.11)

то есть двойной интеграл представляет собой объем так называемого цилиндроида, ограниченного сверху поверхностью z = f(x, y) , а снизу – областью D .

Вычисление двойного интеграла путем сведения его к повторному.

Рассмотрим область D , ограниченную линиями x = a, x = b (a < b ), где φ 1 (х ) и φ 2 (х ) непрерывны на [a, b ]. Тогда любая прямая, параллельная координатной оси Оу и проходящая через внутреннюю точку области D , пересекает границу области в двух точках: N 1 и N 2 (рис.1). Назовем такую область правильной в на-

у правлении оси Оу . Аналогично определя-

y=φ 2 (x )ется область, правильная в направлении

N 2 оси Ох . Область, правильную в направле-

Нии обеих координатных осей, будем на-

D зывать просто правильной. Например,

правильная область изображена на рис.1.

y=φ 1 (x ) N 1

O a b x

Пусть функция f(x, y) непрерывна в области D . Рассмотрим выражение

, (24.12)

называемое двукратным интегралом от функции f(x, y) по области D . Вычислим вначале внутренний интеграл (стоящий в скобках) по переменной у , считая х постоянным. В результате получится непрерывная функция от х :

Полученную функцию проинтегрируем по х в пределах от а до b . В результате получим число

Докажем важное свойство двукратного интеграла.

Теорема 1. Если область D , правильная в направлении Оу , разбита на две области D 1 и D 2 прямой, параллельной оси Оу или оси Ох , то двукратный интеграл по области D будет равен сумме таких же интегралов по областям D 1 и D 2:

Доказательство.

а) Пусть прямая х = с разбивает D на D 1 и D 2 , правильные в направлении Оу . Тогда

б) Пусть прямая y = h разбивает D на правильные в направлении Оу области D 1 и D 2 (рис.2). Обозначим через M 1 (a 1 , h ) и M 2 (b 1 , h ) точки пересечения прямой y = h с гра-ницей L области D .

y Область D 1 ограничена непрерывными линиями

y=φ 2 (x ) 1) y = φ 1 (x );

D 2 2) кривой А 1 М 1 М 2 В , уравнение которой запишем

h M 1 M 2 y = φ 1 *(x ), где φ 1 *(х ) = φ 2 (х ) при а ≤ х ≤ а 1 и

A 1 D 1 B b 1 ≤ x ≤ b , φ 1 *(х ) = h при а 1 ≤ х ≤ b 1 ;

3) прямыми x = a , x = b .

Область D 2 ограничена линиями y = φ 1 *(x ),

A у = φ 2 (х ), а 1 ≤ х ≤ b 1 .

y=φ 1 (x ) Применим к внутреннему интегралу теорему о

разбиении промежутка интегрирования:

O a a 1 b 1 b

Представим второй из полученных интегралов в виде суммы:

+ + .

Поскольку φ 1 *(х ) = φ 2 (х ) при а ≤ х ≤ а 1 и b 1 ≤ x ≤ b , первый и третий из полученных интегралов тождественно равны нулю. Следовательно,

I D = , то есть .

ДВОЙНЫЕ ИНТЕГРАЛЫ

ЛЕКЦИЯ 1

Двойные интегралы. Определение двойного интеграла и его свойства. Повторные интегралы. Сведение двойных интегралов к повторным. Расстановка пределов интегрирования. Вычисление двойных интегралов в декартовой системе координат.

Двойной интеграл представляет собой обобщение понятия определенного интеграла на случай функции двух переменных. В этом случае вместо отрезка интегрирования будет присутствовать какая-то плоская фигура.

Пусть D – некоторая замкнутая ограниченная область, а f (x,y ) – произвольная функция, определенная и ограниченная в этой области. Будем предполагать, что границы области D состоят из конечного числа кривых, заданных уравнениями вида y =f (x ) или x =g(y ), где f (x ) и g (y ) – непрерывные функции.

Разобьем область D произвольным образом на n частей. Площадь i -го участка обозначим символом Ds i . На каждом участке произвольно выберем какую-либо точку P i , и пусть она в какой-либо фиксированной декартовой системе имеет координаты (x i ,y i ). Составим интегральную сумму для функции f (x,y ) по области D, для этого найдем значения функции во всех точках P i , умножим их на площади соответствующих участков Ds i и просуммируем все полученные результаты:

Назовем диаметром diam (G ) области G наибольшее расстояние между граничными точками этой области.

Двойным интегралом функции f (x,y ) по области D называется предел, к которому стремится последовательность интегральных сумм (1.1) при неограниченном увеличении числа разбиений n (при этом ). Это записывают следующим образом

Заметим, что, вообще говоря, интегральная сумма для заданной функции и заданной области интегрирования зависит от способа разбиения области D и выбора точек P i . Однако если двойной интеграл существует, то это означает, что предел соответствующих интегральных сумм уже не зависит от указанных факторов. Для того чтобы двойной интеграл существовал (или, как говорят, чтобы функция f (x,y ) была интегрируемой в области D), достаточно чтобы подынтегральная функция была непрерывной в заданной области интегрирования .

Пусть функция f (x,y ) интегрируема в области D . Поскольку предел соответствующих интегральных сумм для таких функций не зависит от способа разбиения области интегрирования, то разбиение можно производить при помощи вертикальных и горизонтальных линий. Тогда большинство участков области D будет иметь прямоугольный вид, площадь которых равна Ds i =Dx i Dy i . Поэтому дифференциал площади можно записать в виде ds=dxdy . Следовательно, в декартовой системе координат двойные интегралы можно записывать в виде

Замечание . Если подынтегральная функция f (x,y )º1, то двойной интеграл будет равен площади области интегрирования:

Отметим, что двойные интегралы обладают такими же свойствами, что и определенные интегралы. Отметим некоторые из них.

Свойства двойных интегралов.

1 0 . Линейное свойство. Интеграл от суммы функций равен сумме интегралов :

и постоянный множитель можно выносить за знак интеграла :

2 0 . Аддитивное свойство. Если область интегрирования D разбить на две части, то двойной интеграл будет равен сумме интегралов по каждой этой части :

3 0 . Теорема о среднем. Если функция f(x,y ) непрерывна в области D, то в этой области найдется такая точка (x,h), что :

Далее возникает вопрос: как вычисляются двойные интегралы? Его можно вычислить приближенно, с этой целью это разработаны эффективные методы составления соответствующих интегральных сумм, которые затем вычисляются численно при помощи ЭВМ. При аналитическом вычислении двойных интегралов их сводят к двум определенным интегралам.

Для функции двух переменных, заданной как z = f (x , y ) .

Записывается двойной интеграл так:

Здесь D – плоская фигура, ограниченная линиями, выражения которых (равенства) даны в задании вычисления двойного интеграла. Слева и справа – равенствами, в которых слева переменная x , а сверху и снизу – равенствами, в которых слева переменная y . Это место и далее – одно из важнейших для понимания техники вычисления двойного интеграла.

Вычислить двойной интеграл - значит найти число, равное площади упомянутой фигуры D .

Пока мы не касаемся определения двойного интеграла , а будем учиться его вычислять. Понять, что такое двойной интеграл, проще, когда решены несколько задач на его вычисление, поэтому определение двойного интеграла вы найдёте в конце этого урока. Чуть забегая вперёд, можно лишь отметить, что определение двойного интеграла также связано с упоминавшейся фигурой D .

В случае если фигура D представляет собой прямоугольник, все линии, ограничивающие её – это прямые линии. Если фигура D - криволинейна, то слева и справа она ограничена прямыми, а сверху и снизу – кривыми линиями, заданными равенствами, которые даны в задании. Бывают и случаи, когда фигура D – треугольник, но о таких случаях чуть дальше.

Для вычисления двойного интеграла нужно, таким образом, рассортировать линии, огранивающие фигуру D , которая имеет строгое название – область интегрирования. Рассортировать на левые и правые и на верхние и нижние. Это потребуется при сведении двойного интеграла к повторному интегралу – методе вычисления двойного интеграла.

Случай прямоугольной области:

Случай криволинейной области:

А это уже решение знакомых нам определённых интегралов , в которых заданы верхний и нижний пределы интегрирования. Выражения, задающие линии, которые ограничивают фигуру D , будут пределами интегрирования для обычных определённых интегралов, к которым мы уже подходим.

Сведение двойного интеграла к повторному

Случай прямоугольной области

Пусть для такой функции существует двойной интеграл

Чтобы вычислить этот двойной интеграл , нужно свести его к повторному интегралу, который имеет вид

Сначала нужно вычислять внутренний (правый) определённый интеграл, затем - внешний (левый) определённый интеграл.

Можно и поменять ролями x и y

Пример 1. Вычислить двойной интеграл

Вычисляем внутренний (правый) интеграл, считая игрек константой. Получаем.

Пример 2. Вычислить двойной интеграл

Решение. Сводим данный двойной интеграл к повторному интегралу

На чертеже строим область интегрирования:

Теперь вычисляем внешний (левый) интеграл от вычисленного только что внутреннего (правого):

Результат и будет решением данного двойного интеграла.

Вычислить двойной интеграл самостоятельно, а затем посмотреть решение

Случай криволинейной или треугольной области

Пусть снова дана функция двух переменных f (x , y ) , а ограничения для D : уже несколько другого вида:

Эта запись означает, что фигуру D слева и справа ограничивают, как и в случае прямолинейной области - прямые x = a и x = b , но снизу и сверху - кривые, которые заданы уравнениями и . Иными словами, и - функции.

Пусть для такой функции также существует двойной интеграл

Чтобы вычислить этот двойной интеграл, нужно свести его к повторному интегралу, который имеет вид

Здесь пределы интегрирования a и b - числа, а и - функции. В случае треугольной области одна из функций или - это уравнение прямой линии. Такой случай будет разобран в примере 3.

Как и в случае прямолинейной области, сначала нужно вычислять правый определённый интеграл, затем - левый определённый интеграл.

Точно так же можно поменять ролями x и y . Тогда повторный интеграл будет иметь вид

Такой повторный интеграл нужно решать точно так же: сначала - внутренний (правый) интеграл, затем - внешний (левый).

Пример 5. Вычислить двойной интеграл

Решение. Сводим данный двойной интеграл к повторному интегралу

На чертеже строим область интегрирования и видим, что она треугольная:

Вычисляем внутренний (правый) интеграл, считая икс константой. Получаем.

Теперь вычисляем внешний (левый) интеграл от вычисленного только что внутреннего (правого). Сначала представляем этот интеграл в виде суммы интегралов:

Вычисляем первое слагаемое:

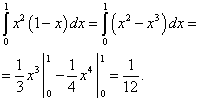
Вычисляем второе слагаемое:

Вычисляем третье слагаемое:

Получаем сумму, которая и будет решением данного двойного интеграла:

Пример 6. Вычислить двойной интеграл

Решение. Сводим данный двойной интеграл к повторному интегралу

На чертеже строим область интегрирования:

Вычисляем внутренний (правый) интеграл, считая икс константой. Получаем.

Теперь вычисляем внешний (левый) интеграл от вычисленного только что внутреннего (правого):

Результат и будет решением данного двойного интеграла.

x -правильная и неправильная, y -правильная и неправильная области интегрирования

Случается, область интегрирования двойного интеграла ограничена такими линиями, что возникает необходимость разбить область интегрирования на части и решать каждый соответствующий повторный интеграл отдельно. Это случаи, когда:

1) область интегрирования представляет собой фигуру, имеющую в виде нижней или верхней (левой или правой) границы две или более двух прямых или кривых линий;

2) область интегрирования представляет собой фигуру, границу которой прямые пересекают более чем в двух точках.

Если вышесказанное относится к левой или правой границе области интегрирования, то есть ограничениях, заданных линиями, выраженными через x , то область интегрирования называется x -неправильной. Если же прямая y = y 0 пересекает соответствующую границу лишь в одной точке и если границей служит лишь одна прямая или кривая, то область интегрирования называется x -правильной

Аналогично, если границу, заданную линиями, выраженными через y , прямая x = x 0 пересекает более чем в одной точке или если границей служат более одной прямой или кривой, то область интегрирования называется y -неправильной. Вывести теперь признаки y -правильной области, надо полагать, совсем просто.

До сих пор мы рассматривали примеры с x -неправильными и y -правильными областями интегрирования. Теперь рассмотрим случаи, когда условие правильности нарушается.

Пример 7. Вычислить двойной интеграл , область интегрирования которого ограничена линиями y = x , xy = 1 , y = 2 .

Решение. Область интегрирования является y -неправильной, так как её нижнюю границу нельзя задать одной линией y = y (x ) . Как видно на рисунке выше, нижняя граница складывается из y = x (тёмно-бордовая) и xy = 1 (зелёная). Поэтому прямой x = 1 (чёрная) можем разбить область интегрирования на две части - и .

Вычисляется этот двойной интеграл так:

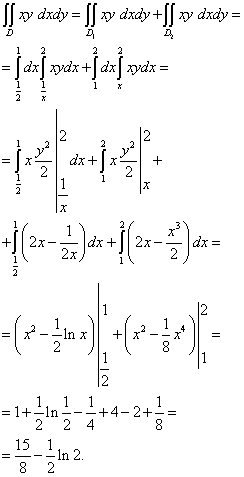
Смена порядка интегрирования

Как уже отмечалось выше, после приведения двойного интеграла к повторному интегралу, можно поменять переменные x и y ролями, или, говоря иначе, поменять порядок интегрирования.

Смена порядка интегрирования образно может быть описана следующими словами О"Генри: "Так ведёт себя обитатель джунглей - зверь, попав в клетку, и так ведёт себя обитатель клетки - человек, заблудившись в джунглях сомнений". Результат, так же по О"Генри один и тот же: "Чалмерс разорвал письмо на тысячу мельчайших клочков и принялся терзать свой дорогой ковёр, расхаживая по нему взад и вперёд". (О"Генри . Шехерезада с Мэдисон-сквера .)

Тогда, если левый интеграл у нас по переменной x , а правый - по y , то после смены порядка интегрирования всё будет наоборот. Тогда пределы интегрирования для "нового" игрека нужно "позаимствовать" у "старого" икса, а пределы интегрирования для "нового" икса получить в виде обратной функции , разрешив относительно икса уравнение, задававшее предел для игрека.

Пример 8.

Решение. После смены порядка интегрирования интеграл по игреку станет левым, а интеграл по иксу - правым. Пределы интегрирования для "нового" игрека позаимствуем у "старого" икса, то есть нижний предел равен нулю, а верхний - единице. Пределы интегрирования для "старого" игрека заданы уравнениями и . Разрешив эти уравнения относительно икса, получим новые пределы интегрирования для икса:

(нижний) и (верхний).

Таким образом, после смены порядка интегрирования повторный интеграл запишется так:

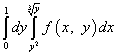После смены порядка интегрирования в двойном интеграле нередко область интегрирования превращается в y -неправильную или x -неправильную (см. предыдущий параграф). Тогда требуется разбить область интегрирования на части и решать каждый соответствующий повторный интеграл отдельно.

Поскольку разбиение области интегрирования на части представляет определённые трудности для многих студентов, то не ограничимся примером, приведённым в предыдущем параграфе, а разберём ещё пару примеров.

Пример 9. Сменить порядок интегрирования для повторного интеграла

Решение. Итак, область интегрирования данного повторного интеграла ограничена прямыми y = 1 , y = 3 , x = 0 , x = 2y .

При интегрировании в другом порядке нижняя граница области состоит из двух прямых: AB и BC , которые заданы уравнениями y = 1 и y = x /2 , что видно на рисунке ниже.

Выход из такой неопределённости состоит в разбиении области интегрирования на две части. Делить область интегрирования будет прямая BМ . Новые пределы интегрирования вычисляем, находя обратную функцию. Соответственно этому решению повторный интеграл после смены порядка интегрирования будет равным сумме двух интегралов:

Естественно, таким же будет решение двойного интеграла, который сводится к повторному интегралу, данному в условии этого примера.

Пример 10. Сменить порядок интегрирования для повторного интеграла

Решение. Итак, область интегрирования повторного интеграла ограничена прямыми x = 0 , x = 2 и кривыми и .

Как видно на рисунке ниже, прямая, параллельная оси 0x , будет пересекать нижнюю границу области интегрирования более чем в двух точках.

Поэтому разобьём область интегрирования на три части прямыми, которые на рисунке начерчены чёрным. Новые пределы интегрирования вычисляем, находя обратную функцию. Пределы для трёх новых областей интегрирования будут следующими.

Соответственно этому решению повторный интеграл после смены порядка интегрирования будет равным сумме трёх интегралов:

Той же сумме трёх интегралов будет равен и двойной интеграл, который сводится к повторному интегралу, данному в условии этого примера.

И всё же обстоятельства непреодолимой силы нередко мешают студентам уже на предыдущем шаге - расстановке пределов интегрирования. Тревога и смятение не лишены некоторого основания: если для разбиения области интегрирования на части обычно достаточно приглядеться к чертежу, а для решения повторного интеграла - таблицы интегралов, то в расстановке пределов интегрирования нужен некоторый опыт тренировок. Пробежим пример, в котором остановимся только на расстановке пределов интегрирования и - почти на автомате - на разбиении области и опустим само решение.

Пример 11. Найти пределы интегрирования двойного интеграла, если область интегрирования D задана следующим образом:

y - 2x ≤ 0;
2y - x ≥ 0;
xy ≤ 2.

Решение. В явном виде (через x и y "без примесей") линии, ограничивающие область интегрирования, не заданы. Так как для икса ими чаще всего оказываются прямые, касающиеся в одной точке верхней и нижней границ, выраженных через игрек, то пойдём именно по этому пути. Тем более, что при смене порядка интегирования мы получим область интегрирования с такой же площадью. Разрешим неравенства относительно игрека и получим:

y ≤ 2x ;
y ≥ x /2;
y ≤ 2/x .

Строим полученные линии на чертёже. Пределами интегрирования по иксу действительно служат линии x = 0 и x = 2 . Но область интегрирования оказалась y -неправильной, так как её верхнюю границу нельзя задать одной линией y = y (x ) .

Основные свойства двойного интеграла

Свойства двойного интеграла (и их вывод) аналогичны соответствующим свойствам однократного определенного интеграла.

1° . Аддитивность . Если функция f (x , y ) интегрируема в области D и если область D при помощи кривой Г площади нуль разбивается на две связные и не имеющие общих внутренних точек области D 1 и D 2 , то функция f (x , y ) интегрируема в каждой из областей D 1 и D 2 , причем

2° . Линейное свойство . Если функции f (x , y ) и g (x , y ) интегрируемы в области D , а α и β - любые вещественные числа, то функция [α · f (x , y ) + β · g (x , y )] также интегрируема в области D , причем

3° . Если функции f (x , y ) и g (x , y ) интегрируемы в области D , то и произведение этих функций интегрируемо в D .

4° . Если функции f (x , y ) и g (x , y ) обе интегрируемы в области D и всюду в этой области f (x , y ) ≤ g (x , y ), то

5° . Если функция f (x , y ) интегрируема в области D , то и функция |f (x , y )| интегрируема в области D , причем

(Конечно, из интегрируемости |f (x , y )| в D не вытекает интегрируемость f (x , y ) в D .)

6° . Теорема о среднем значении . Если обе функции f (x , y ) и g (x , y ) интегрируемы в области D , функция g (x , y ) неотрицательна (неположительна) всюду в этой области, M и m - точная верхняя и точная нижняя грани функции f (x , y ) в области D , то найдется число μ , удовлетворяющее неравенству m ≤ μ ≤ M и такое, что справедлива формула

Задача, приводящая к понятию двойного интеграла.

Предположим, что на определена функция частей и запишем сумму

которая именуется интегральной.

О: Под определенным интегралом (о.и.) от функции и от выбора

Обозначение:

Числа именуют интегрируемой (по Риману) на .

Т. существования: При условии, что .

В соответствии с определением о.и. отметим, что интеграл имеет зависимость от вида , пределов и , однако не зависит от символа обозначения переменной , иначе выражаясь

В соответствии с п.17.1.1 и 17.1.2 и определением о.и. запишем формулы площади криволинейной трапеции: , работы силы

на :

Понятие двойного интеграла, интегральных сумм.

Существование двойного интеграла, т. е. предела интегральной суммы для кажется очевидным, так как этот предел дает объем цилиндрического тела. Однако это рассуждение не является строгим. В более полных курсах это утверждение строго доказывается и носит название теоремы существования двойного интеграла.

Теорема существования. Для всякой функции, непрерывной в ограниченной замкнутой области, имеющей площадь а, существует двойной интеграл, т. е. существует предел интегральных сумм при неограниченном увеличении числа малых площадок при условии, что каждая из них стягивается в точку. Этот предел не зависит ни от способа разбиения области а на части ни от выбора точек

В дальнейшем мы будем рассматривать только функции, непрерывные в области интегрирования.

Из теоремы существования следует, что мы можем, например, разбить область а на малые прямоугольники со сторонами прямыми, параллельными осям координат (рис. 230). При этом. Выбирая затем в каждом малом прямоугольнике по точке мы можем написать, согласно определению двойного интеграла

Для того чтобы подчеркнуть, что двойной интеграл можно получить как предел суммы вида вместо обозначения употребляют также обозначение

Выражение называется элементом площади в декартовых координатах и равно площади прямоугольника со сторонами параллельными координатным осям.

Заметим, что при составлении интегральной суммы площадки прилегающие к границе области а, не имеют формы прямоугольников. Однако можно доказать, что ошибка от замены таких площадок прямоугольниками с площадями в пределе сведется к нулю.

Свойства двойных интегралов

3° . Если функции f (x , y ) и g (x , y ) интегрируемы в области D , то и произведение этих функций интегрируемо в D .

4° . Если функции f (x , y ) и g (x , y ) обе интегрируемы в области D и всюду в этой области f (x , y ) ≤ g (x , y ), то

5° . Если функция f (x , y ) интегрируема в области D , то и функция |f (x , y )| интегрируема в области D , причем

(Конечно, из интегрируемости |f (x , y )| в D не вытекает интегрируемость f (x , y ) в D .)

В частности, если функция f (x , y ) непрерывна в D , а область D связна , то в этой области найдется такая точка (ξ , η ), что μ = f (ξ , η ), и формула (11) принимает вид